PESO DE MATERIALES

TIPOS DE CARGAS

FUERZAS APLICADAS A UNA ESTRUCTURA.

Se distinguen dos tipos de fuerzas actuando en un cuerpo: las externas y las internas.

Las externas son las actuantes o aplicadas exteriormente y las reacciones o resistentes que impiden el movimiento.

Las internas son aquellas que mantienen el cuerpo o estructura como un ensamblaje único y corresponden a las fuerzas de unión entre sus partes.

Las actuantes son aquellas cargas a las que se ve sometida la estructura por su propio peso, por la función que cumple y por efectos ambientales. En primera instancia se pueden subdividir en cargas gravitacionales, cargas hidrostáticas y fuerzas ambientales (sismo, viento y temperatura).

Las gravitacionales son aquellas generadas por el peso propio y al uso de la estructura y se denominan gravitacionales porque corresponden a pesos. Entre ellas tenemos las cargas muertas y las cargas vivas.

Otra clasificación de las cargas es por su forma de aplicación: dinámicas y estáticas.

Las cargas dinámicas son aquellas aplicadas súbitamente y causan impacto sobre la estructura. Las cargas estáticas corresponden a una aplicación gradual de la carga.

CARGAS GRAVITACIONALES

1 Cargas muertas

Son cargas permanentes y que no son debidas al uso de la estructura. En esta categoría se pueden clasificar las cargas correspondientes al peso propio y al peso de los materiales que soporta la estructura tales como acabados, divisiones, fachadas, techos, etc. Dentro de las cargas muertas también se pueden clasificar aquellos equipos permanentes en la estructura. En general las cargas muertas se pueden determinar con cierto grado de exactitud conociendo la densidad de los materiales.

2 Cargas vivas

Corresponden a cargas gravitacionales debidas a la ocupación normal de la estructura y que no son permanentes en ella. Debido a la característica de movilidad y no permanencia de esta carga el grado de incertidumbre en su determinación es mayor. La determinación de la posible carga de diseño de una edificación ha sido objeto de estudio durante muchos años y gracias a esto, por medio de estadísticas, se cuenta en la actualidad con una buena aproximación de las cargas vivas de diseño según el uso de la estructura. Las cargas vivas no incluyen las cargas ambientales como sismo o viento.

Para efectos de diseño es el calculista quien debe responder por la seguridad de la estructura en su vida útil, para esto cuenta con las ayudas de las normas y códigos de diseño donde se especifican las cargas vivas mínimas a considerar.

Módulo de elasticidad del acero

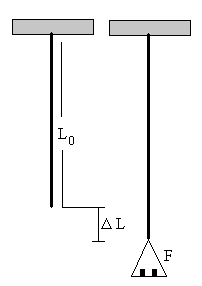Un hilo metálico sometido a un esfuerzo de tracción sufre una deformación que consiste en el aumento de longitud y en una contracción de su sección. Supondremos que el aumento de longitud es el efecto dominante, sobre todo en hilos largos y de pequeña sección. Estudiaremos el comportamiento elástico de los hilos, aquél en el que existe una relación de proporcionalidad entre la fuerza Faplicada al hilo y el incremento DL de su longitud o bien, entre el esfuerzo F/S y la deformación unitaria DL/L0.

Donde S es la sección del hilo S=p r², y Y es una constante de proporcionalidad característica de cada material que se denomina módulo de elasticidad o módulo de Young.

Metal	Módulo de Young, Y·1010 N/m2
Cobre estirado en frío	12.7
Cobre, fundición	8.2
Cobre laminado	10.8
Aluminio	6.3-7.0
Acero al carbono	19.5-20.5
Acero aleado	20.6
Acero, fundición	17.0
Cinc laminado	8.2
Latón estirado en frío	8.9-9.7
Latón naval laminado	9.8
Bronce de aluminio	10.3
Titanio	11.6
Níquel	20.4
Plata	8.27

Fuente: Koshkin N. I., Shirkévich M. G.. Manual de Física Elemental. Editorial Mir 1975.

Representando el esfuerzo en función de la deformación unitaria para un metal obtenemos una curva característica semejante a la que se muestra en la figura. Durante la primera parte de la curva, el esfuerzo es proporcional a la deformación unitaria, estamos en la región elástica. Cuando se disminuye el esfuerzo, el material vuelve a su longitud inicial. La línea recta termina en un punto denominado límite elástico.

Si se sigue aumentando el esfuerzo la deformación unitaria aumenta rápidamente, pero al reducir el esfuerzo, el material no recobra su longitud inicial. La longitud que corresponde a un esfuerzo nulo es ahora mayor que la inicial L₀, y se dice que el material ha adquirido una deformación permanente.

El material se deforma hasta un máximo, denominado punto de ruptura. Entre el límite de la deformación elástica y el punto de ruptura tiene lugar la deformación plástica.

Si entre el límite de la región elástica y el punto de ruptura tiene lugar una gran deformación plástica el material se denomina dúctil. Sin embargo, si la ruptura ocurre poco después del límite elástico el material se denomina frágil.

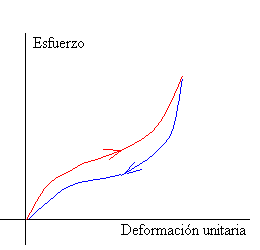En la figura, se representa el comportamiento típico de esfuerzo - deformación unitaria de un material como el caucho. El esfuerzo no es proporcional a la deformación unitaria (curva de color rojo), sin embargo, la sustancia es elástica en el sentido que si se suprime la fuerza sobre el material, el caucho recupera su longitud inicial. Al disminuir el esfuerzo la curva de retorno (en color azul) no es recorrida en sentido contrario. La falta de coincidencia de las curvas de incremento y disminución del esfuerzo se denomina histéresis elástica. Un comportamiento análogo se encuentra en las sustancias magnéticas.

Puede demostrarse que el área encerrada por ambas curvas es proporcional a la energía disipada en el interior del material elástico. La gran histéresis elástica de algunas gomas las hace especialmente apropiadas para absorber las vibraciones.

Medida del módulo de elasticidad

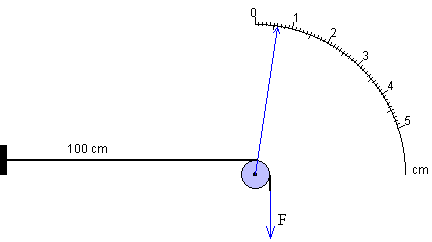
En la figura, se muestra el dispositivo experimental. Se emplea un hilo de un metro de longitud dispuesto horizontalmente fijado por un extremo, mientras que el otro pasa por una polea. Del extremo libre se cuelgan pesas de 100 g, 250 g ó 500 g.

Al poner pesas sobre el extremo libre del hilo, el alambre se alarga y la polea gira un ángulo igual a DL/r. Siendo r el radio de la polea.

Como el alargamiento DL es pequeño, se puede medir mediante una aguja indicadora que marca sobre un sector circular cuyo radio es R=10·r veces el radio de la polea.

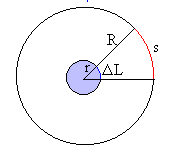Como vemos en la figura, las longitudes de los arcos son proporcionales a los radios, de modo que El arco s es 10 veces mayor que el alargamiento DL

Módulo de elasticidad del concreto

El concreto no es un material eminentemente elástico, esto se puede observar fácilmente si se somete a un espécimen a esfuerzos de compresión crecientes hasta llevarlo a la falla, si para cada nivel de esfuerzo se registra la deformación unitaria del material, se podría dibujar la curva que relaciona estos parámetros, la Figura 9.15 muestra la curva esfuerzo-deformación (expresada en ocasiones como la curva).

Figura 9.15. Curva Típica Esfuerzo-Deformación para el Concreto Bajo Compresión, y Puntos para Definir el Módulo de Elasticidad según ASTM C-469.

De la Figura 9.15, y de acuerdo a la norma ASTM C-469, el módulo de elasticidad (Ec) se obtiene calculando la pendiente del segmento de recta que pasa por los puntos A y B, para lo cual es necesario obtener del trazo de la curva (o en el transcurso de la prueba) la ordenada correspondiente a las 50 microdeformaciones y la abscisa correspondiente al esfuerzo 0.40f’c. De la figura se observa también que la deformación que corresponde a la resistencia del concreto es 0.002 cm/cm, que corresponde a 2,000 microdeformaciones. Aún después de que el concreto alcanza su resistencia máxima, y si la carga se sostiene (el esfuerzo disminuye) hasta lograr la falla total (el concreto truena), se puede medir la deformación última que soporta el material, ésta deformación es de 0.035 cm/cm.
Pruebas como la del módulo de elasticidad del concreto son bastante tediosas si se realizan con instrumentaciones anticuadas, ya que el factor humano es determinante para la toma secuencial de lecturas tanto de carga como de deformaciones, por ese motivo se aconseja emplear una instrumentación adecuada como la mostrada en la Figura 9.16, donde se observa que se han conectado al cilindro de prueba un medidor de deformaciones electrónico conocido LVDT (Linear Variable Differential Transformer) con el cual se miden las deformaciones verticales, estas deformaciones se registran automáticamente por medio de una computadora conectada al medidor, y por medio de un programa se puede graficar la curva σ -ε y calcular al mismo tiempo el módulo de elasticidad.

Figura 9.16. Determinación del Módulo de Elasticidad del Concreto.

El módulo de elasticidad es un parámetro muy importante en el análisis de las estructuras deconcreto ya que se emplea en el cálculo de la rigidez de los elementos estructurales, en algunos lugares como en la ciudad de México y a raíz de los terremotos de 1985, se han echo cambios en el Reglamento de construcciones del Distrito Federal, estos cambios demandan valoresmínimos para el módulo de elasticidad dependiendo del tipo de concreto que se emplee en laobra, por lo tanto ahora, además de la f’c se debe garantizar Ec. En algunos estructuristas existe latendencia a suponer valores de Ec, para lo cual emplean fórmulas sugeridas por diversasinstituciones, por ejemplo el Comité Aci-318 sugiere en su reglamento la siguiente ecuación paraconcretos de 90 a 155 lb/pie3:

Cualquiera que sea la expresión que se use, no se debe perder de vista que el valor que se obtenga es útil solamente a nivel de anteproyecto, para el proyecto final de una obra se debe emplear el módulo de elasticidad del concreto que realmente estará en la obra, esto sólo es posible si el estructurista tiene el cuidado de recabar la información del productor local del concreto, o en su defecto se deben cotizar las pruebas respectivas con cargo al trabajo de análisis y diseño. Es muy peligroso para la seguridad de la estructura emplear indiscriminadamente fórmulas cuando se desconocen las características elásticas del concreto que se puede fabricar en la zona donde se construirá la obra.

LOSAS RETICULADAS

Este tipo de losas se elabora a base de un sistema de entramado de trabes cruzadas que forman una retícula, dejando huecos intermedios que pueden ser ocupados permanentemente por bloques huecos o materiales cuyo peso volumétrico no exceda de 900kg/m y sean capaces de resistir una carga concentrada de una tonelada. La combinación de elementos prefabricados de concreto simple en forma de cajones con nervaduras de concreto reforzado colado en el lugar que forman una retícula que rodea por sus cuatro costados a los bloques prefabricados. También pueden colocarse, temporalmente a manera de cimbra para el colado de las trabes, casetones de plástico prefabricados que una vez fraguado el concreto deben retirarse y lavarse para usos posteriores. Con lo que resulta una losa liviana, de espesor uniforme.

Entre sus ventajas se encuentra
• Los esfuerzos de flexión y corte son relativamente bajos y repartidos en grandes areas.
• Permite colocar muros divisorios libremente.
• Se puede apoyar directamente sobre las columnas sin necesidad de trabes de carga entre columna y columna.
• Resiste fuertes cargas concentradas, ya que se distribuyen a areas muy grandes a través de las nervaduras cercanas de ambas direcciones.
• Las losas reticulares son más livianas y más rígidas que las losas macizas.
• El volumen de los colados en la obra es reducido.
• Mayor duración de la madera de cimbra, ya que sólo se adhiere a las nervaduras, y puede utilizarse más veces
• Este sistema reticular celulado da a las estructuras un aspecto agradable de ligereza y esbeltez.
• El entrepiso plano por ambas caras le da un aspecto mucho más limpio a la estructura y permite aprovechar la altura real que hay de piso a techo para el paso de luz natural. La superficie para acabados presenta características óptimas para que le yeso se adhiera perfectamente, dejando una superficie lisa, sin ocasionar grietas.

TIPOS DE FORJADOS

La clasificación de los forjados se puede realizar atendiendo a distintos criterios.

a). Según el sistema de transmisión de cargas los forjados se clasifican en:

- Unidireccionales: Flectan básicamente en una dirección y transmiten las cargas a las vigas, y éstas, a los soportes. Una variante muy utilizada en la actualidad son las losas macizas apoyadas en muros, según el sistema «encofrados túnel» o alguno de sus derivados.

Bidireccionales: Flectan en dos direcciones y transmiten las cargas a las vigas en dos direcciones (placas sobre vigas en dos direcciones, figura 5), o bien directamente a los pilares

b). Según su constitución se clasifican en:

- Forjados de viguetas resistentes con bovedillas y relleno de senos.

- Forjados de semiviguetas con bovedillas y relleno de senos

- Forjados de semiviguetas en celosía

- Forjados de viguetas dobles


c). Por el sistema de ejecución, los forjados se clasifican en:

- Forjados construidos totalmente in situ.

- Forjados semiprefabricados. Constituidos por viguetas o semiviguetas, piezas de entrevigado y hormigón colocado in situ, con sus correspondientes armaduras. En las figuras 7, 8, 9 y 10 se muestran algunas
de las soluciones de uso más frecuente.

- Forjados prefabricados. Sólo es preciso proceder a su montaje en obra, o como máximo realizar pequeñas operaciones de relleno de juntas.

d). Por el grado de hiperestatismo, los forjados se clasifican en:

- Forjados simplemente apoyados. Su empleo se reduce casi exclusivamente a cubiertas.

- Forjados continuos. Son los más utilizados y los que cumplen las funciones de dar rigidez transversal a las vigas y solidarizar horizontalmente los entramados a nivel de cada planta.

e). Según su armadura se clasifican en:

- Forjados armados.

- Forjados pretensados. Se realizan con armaduras pretensas casi en su totalidad.

En el caso de los forjados de semiviguetas pretensadas, los momentos negativos son absorbidos con armaduras pasivas, por lo que estamos en un caso de sección compuesta, con armaduras activas pretensas para resistir los momentos positivos y armaduras activas y pasivas para resistir los
momentos negativos.

- Forjados con pretensado parcial, es decir, aquéllos en los que la armadura está constituida simultáneamente por armaduras activas y pasivas.

Definiciones

momento flector negativo: Momento flector que produce una curvatura convexa en una parte de la estructura. También llamado momento negativo.

momento negativo: Momento flector que produce una curvatura convexa en una parte de la estructura. También llamado momento flector negativo.

centro de momento: Punto en el que el eje de un momento corta el plano de las fuerzas que lo producen.

Esfuerzo cortante de punzonamiento

Esfuerzo cortante elevado, debido a la reacción de la fuerza que desarrolla un pilar sobre una losa de hormigón armado.

Esfuerzo cortante horizontal: Esfuerzo cortante que se desarrolla a lo largo de un elemento estructural que es sometido a cargas transversales, que es igual al esfuerzo cortante vertical en ese mismo punto. También llamado esfuerzo cortante longitudinal

torsión horizontal: Torsión que se produce debido a que al actuar una carga lateral sobre una estructura cuyos centros de masas y de resistencia no coinciden.

VARILLAS

La varilla se utiliza como refuerzo del concreto; son barras de acero generalmente circulares y corrugadas con un diámetro superior a los 5 milímetros, aunque comúnmente el diámetro de la varilla se especifica en pulgadas. La superficie de la varilla está provista de rebordes (corrugaciones) que mejoran la adherencia a los materiales aglomerantes e inhiben el movimiento relativo longitudinal entre la varilla y el concreto que la rodea, y de hecho el papel de la varilla corrugada no es sólo reforzar la estructura del concreto armado, sino absorber los esfuerzos de tracción y torsión.

Se fabrica varilla de sección redonda, que pueden ser lisas o estradas, y también de sección cuadrada, más empleadas en herrería.

En México, la varilla corrugada está regida con la norma oficial mexicana NMX-C-407

Nuestra varilla corrugada tiene las siguientes características:

Propiedades Mecánicas
Resistencia a la tensión: 6,300 kg/cm2
Resistencia a la fluencia: 4,200 kg/cm2

Tabla de Dimensiones Nominales

Diámetro
Núm. de Varilla	pulg.	mm.
3	3/8	9.5
4	1/2	12.7
5	5/8	15.9
6	3/4	19
8	1	25.4
10	1 1/4	31.8
12	1 1/2	38.1

Tipos de varillas:

Varillas de alambre de hierro y acero.

Alambre de acero estirado y acero reforzado

Varilla de hierro estirado en frío

Varilla de hierro estañado

Varilla de hierro galvanizado

Varilla de acero

Varilla de acero inoxidable

Varilla de acero aleado

Varilla de acero al cromo

Varilla de acero al cromo molibdeno

Varilla de acero al cromo vanadio

Varilla de acero al molibdeno

Varilla de acero al níquel

Varilla de acero al cromo níquel

Varilla de acero al níquel-molibdeno

Varilla de acero al níquel-cromo-molibdeno

Varilla de acero silicomanganoso

Varilla de acero volframioso rectificado

Varilla de acero rápido

Varilla de acero maquinable

Varilla de acero semicalmado

Varilla de acero ácido

Varilla de acero calmado con aluminio

Varilla de acero calmado con silicio

Varilla de acero efervescente

Varilla de acero ácido termoresistente

Varilla de acero estirado para tuercas y tornillos

Varilla de acero recalcado en frío

Varilla de acero para la industria del automóvil

Varilla de acero para cojinetes de bolas

Varilla hexagonal de acero

Varilla octagonal de acero

Varilla redonda de acero

Alambre de acero para resistencias eléctricas

Varilla de acero en rollos

Barras de refuerzo de acero

Varillas de acero para hormigón armado

Varillas de acero según normas aeronáuticas